k-means 法の注意点とオレオレベストプラクティス
このエントリについて
クラスタリングでよく使われている k-means 法ですが、最近は BI ツールでサポートされていて自称データサイエンティストさんでも誰でもデータを突っ込めば何かしらのクラスタリング結果が得られるわけです。
が、手法の特徴を把握せずに使ってるとひどいクラスタリング結果を量産してしまうことになりかねないよってことと、ではどうすれば失敗を減らせるかというところを書きます。
k-means 法の説明はここではしません。 ある程度どういうものか、何のために使うものかを理解している前提で話を進めますが、 不安のある人は 神嶌先生のサイト なんか見るといいよ。 神嶌先生最高!
ツール紹介
ということで k-means 法の癖を見るためのツール を用意しました。
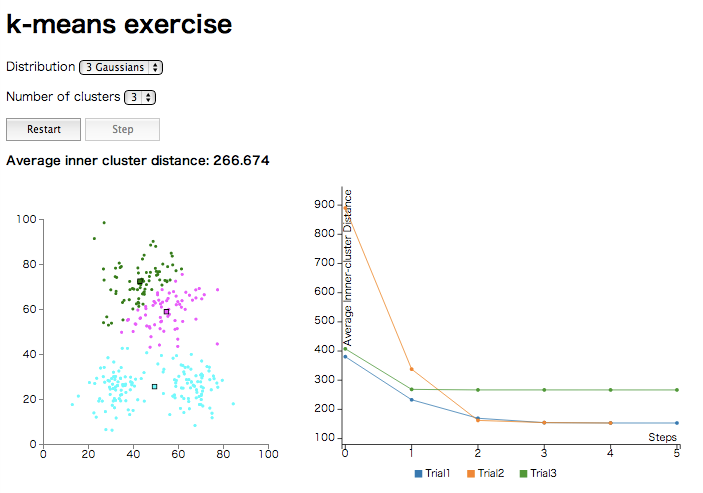
左の散布図で2次元のサンプルデータをユークリッド距離の k-means 法でクラスタリングしていく過程を見ることができます。 サンプルデータの分布とクラスタ数 k は複数から選択できるようにしました。
また、右の折れ線グラフではクラスタのセントロイドからの各サンプルデータまでの距離の2乗の平均、つまり前述の 神嶌先生のサイト における k-means 法の評価関数(をデータ数で割ったもの) *1 のステップごとの推移を表しています。 ランダムの初期値の取り方により、違う推移をしていくことが観察できます。
ちなみにグラフ描画には D3.js と C3.js を使いました。D3.js は説明不要ですね。C3.js はグラフ描画用の D3.js ラッパーライブラリで、今回初めて使ってみました。*2
以下、いくつかの分布で k-means の性質を述べます。
一様分布(Uniform)

一様ランダムなサンプルデータ分布です。
まずはこちらでいろいろ遊んでもらえればと思います。
3つの2次元正規分布(3 Gaussians)

3つの2次元正規分布の確率からなるサンプルデータ分布です。
これを Number of clusters = 3 で何回か実行してみてください。 右の折れ線の収束時の y 軸の高さが、2つの高さに収束するはずです。 このことは、 初期値のランダムの取り方によってクラスタの凝集度が大きく違ってくる ということを示します。
3つの円状分布(3 Circles)

3つの円状の分布からなるサンプルデータ分布です。
見た感じでは結構はっきりと分かれていますね。 これなら Number of clusters = 3 で3つのクラスタにも簡単に分けられるはず。
…と思ったら大間違いで、人間の感覚どおりにきれいに3つに分けることはできません。 ユークリッド距離等の距離尺度を用いる場合、k-means 法ではクラスタ境界はセントロイド同士を結ぶ直線の二等分線となります。 二等分線であり直線上の疎密は考慮しないので、そのような結果となります。 *3
2つの離れた分布(Separated)

少量データからなる2つの隔てられたサンプルデータ分布です。
これを Number of clusters = 2 で2つのクラスタに分けてみてください。 こんな簡単な分布がきれいに分けれない訳がない…と思いますか? これが 1/7 の確率で予想外のクラスタ分布になります。やってみてください。
k-means 法の運用
オレオレベストプラクティス
以上を踏まえると「分析で k-means 法を使わなくちゃいけない><」ってなったときは、次のような運用が安全だと言えます。
- ループはできる限り収束するまで回す
- ある k においてはランダムで初期値を変えて複数回実行し、クラスタ内距離平均のような KPI で最適なクラスタの分け方をみつける
- いくつかの k について上記を試し、おさまりの良さそうな k を決定する
ベストプラクティスとか書きましたが、k-means の性質が分かっていればまあ普通は上記のような方法になるんじゃないの。
クラスタリングの KPI
KPI については今回折れ線グラフで出したものが一番シンプルなものですが、クラスタ内の凝集度だけでなくクラスタ間の離れ具合も考慮した Pseudo-F 、SAS で使われている CCC 、Mahout で採用されている CDbw 等、いろいろあるようです。 これらのどれかを使って 定量的に 評価しないとクラスタリング結果のクオリティは安定しません。
最後に
k-means 法って扱いにくいからやらない方がいいよ…ということではなく、ハサミも使い方分かってないと手を切っちゃいますよね。分析で使う道具についても知っといた方がいいよという話でした。
(ピュアな k-means 法をdisるのは別のエントリでやります^^)